
뉴런을 설계할 수 있는 방법과 모델은 다양하게 존재하지만,
그 중 integrate-and-fire model을 FPGA를 사용하여 구현할 수 있다.
[XOR problem]
뉴로모픽 시스템에서 XOR이란?

XOR이란?
배타적 논리합이라는 뜻으로 두 개의 입력 중 하남나 참일 때, 결과가 참이 되는 논리 연산을 의미한다.
XOR문제는 단층 퍼셉트론으로는 해결할 수 없으며, 선형 분리가 불가능한 문제이다.
단층 퍼셉트론은 AND, OR, NOT 등의 선형 분리가 가능한 문제만 처리할 수 있으므로,
XOR문제를 해결하기 위해서는 다층 퍼셉트론(MLP)과 같이 은닉층(Hidden layer)이 있는 다층 구조가 필요하다.
가장 중요한 내용은 학습 알고리즘을 통한 bias와 weights의 조절이며,
back propagation learning이 일반적으로 사용되고
이는 기대값과 실제 출력값과의 차이를 통해 weights를 보정하는 방법이다.,
Unsupervised learning 방법에 STDP가 있으며, 이는 입력과 동일한 출력을 얻거나 pattern 인식 분야에 효과적이다.
[2 Input Neuron]
Sigmoid 함수 대신, Step 함수를 사용하여 설계할 것이다.
뉴런의 동작 조건
① Multiplier
② Adder
Multiplier 와 Adder의 성능이 중요하며, 많은 부분을 차지한다.
(실제 FPGA에서 구현되는 경우, DSP나 LUT으로 변환된다.)
③ Sigmoid(Activation function)
④ STDP 등의 구현과 저전력 동작을 위해서는
spiking에 따른 frequency가 정보를 담고 있어야 한다.

XOR 동작을 위한 뉴런 -1-
실제 응용에서는 학습은 CPU-GPU가 수행하고, FPGA는 inference로 사용되는 것이 일반적이다.
대신 아래의 동작을 수행하는 뉴런을 설계하고자
(XOR의 경우 여러 가지 해법이 가능하다.)

module Neuron_XOR( input clk, input signed [7:0] a1, a2, input signed [7:0] q1, q2, output reg out = 0, output reg signed [15:0] Vp = 0 ); parameter leak = 16'd1; parameter signed vth = 16'd20; parameter signed reset = 16'd0; always @ (posedge clk) begin Vp = Vp + (a1 * q2) + (a2 * q2); if (Vp > 0) Vp = Vp - leak; if (Vp > vth) begin out = 1; Vp = reset; end else if (Vp <= vth) begin out = 0; end end endmodule
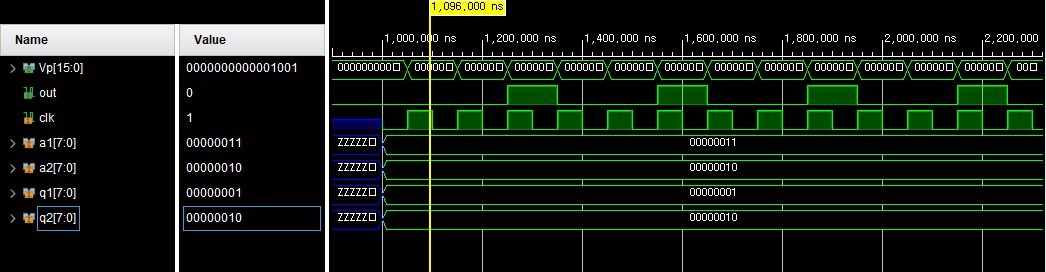
⊙ 2 input neuron의 기본적인 형태
(sigmoid 함수 대신, step 함수 사용)
⊙입력이 signed 8-bit이며, 일정 시간이 지남에 따라 output이 pulse 형태로 출력됨을 알 수 있다.
▶Leaky integrate-and-fire의 기본 형태이다.
XOR 동작을 위한 뉴런 - 2 -
입력이 1 bit이며, weights와 bias는 signed digit이어야 한다.
단순 입력이 출력에 반영되는 Combinational Log의 형태이다.
MUX 형태로 곱셈을 구현하므로, 회로 영역이 작아진다.
module IFm( // XOR 동작을 위한 뉴런 input clk, input a1, a2, input signed [7:0] q1, q2, bias, output reg out = 0, output reg signed [7:0] Vp = 0 ); parameter signed vth = 8'b0000000; parameter signed reset = 8'b00000000; always @ (posedge clk) begin Vp = Vp + ((a1 == 1) ? q1 : 0) + ((a2 == 1) ? q2 : 0) + bias; if (Vp > vth) begin out = 1; Vp = reset; end else if (Vp <= vth) begin out = 0; Vp = reset; end end endmodule
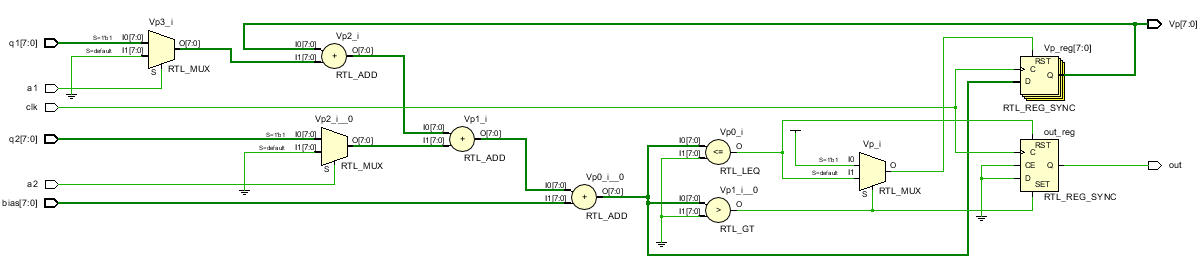
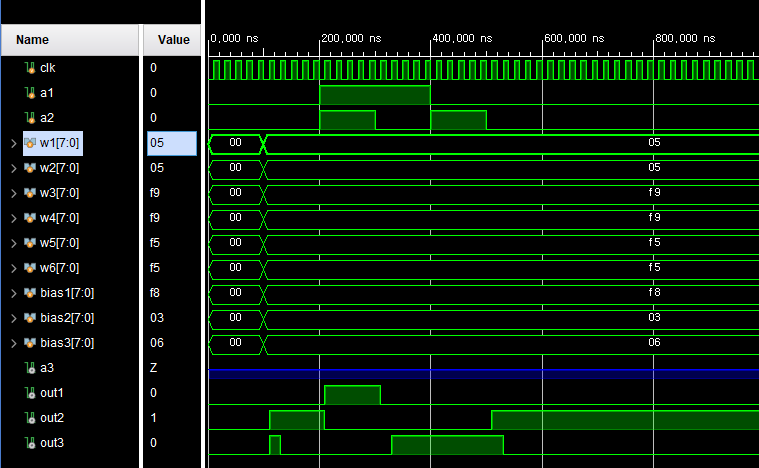
XOR 동작을 위한 뉴럴 네트워크
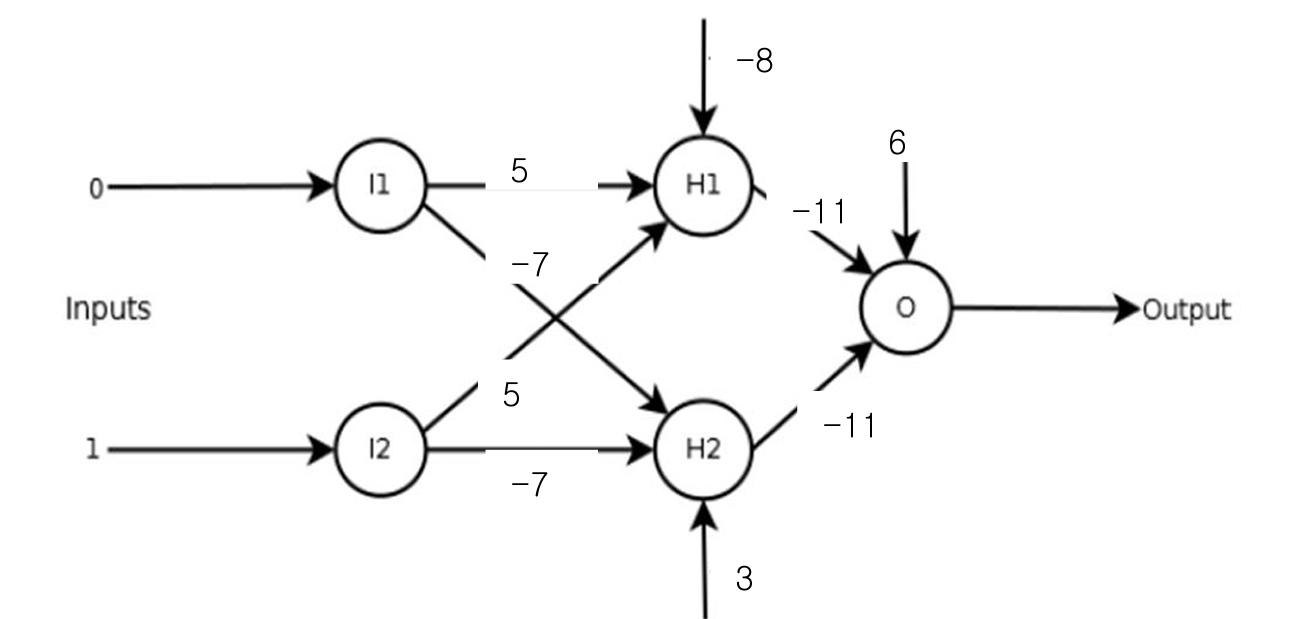
은닉층을 포함하여 3개의 뉴런으로 구성된다.
module net( input clk, input a1, a2, a3, input signed [7:0] w1, w2, w3, w4, w5, w6, bias1, bias2, bias3, output out1, out2, out3 ); IFm n1(.clk(clk), .a1(a1), .a2(a2), .q1(w1), .q2(w2), .bias(bias1), .out(out1) ); IFm n2(.clk(clk), .a1(a1), .a2(a2), .q1(w3), .q2(w4), .bias(bias2), .out(out2) ); IFm n3(.clk(clk), .a1(out1), .a2(out2), .q1(w5), .q2(w6), .bias(bias3), .out(out3) ); endmodule
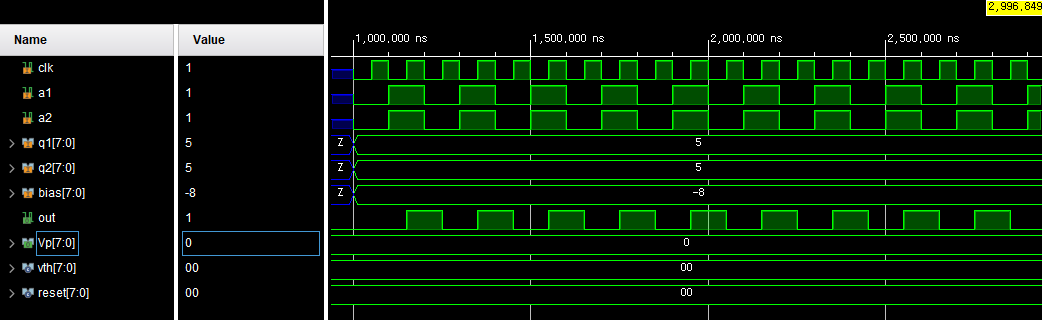
module net_testbench(); reg clk, a1, a2; reg signed [7:0] w1, w2, w3, w4, w5, w6, bias1, bias2, bias3; net DUT (clk, a1, a2, a3, w1, w2, w3, w4, w5, w6, bias1, bias2, bias3, out1, out2, out3); initial clk = 0; always #10 clk = ~clk; initial begin a1 = 0; a2 = 0; w1 = 0; w2 = 0; w3 = 0; w4 = 0; w5 = 0; w6 = 0; bias1 = 0; bias2 = 0; bias3 = 0; #100; w1 = 8'd5; w2 = 8'd5; w3 = -8'd7; w4 = -8'd7; w5 = -8'd11; w6 = -8'd11; bias1 = -8'd8; bias2 = 8'd3; bias3 = 8'd6; #100; a1 = 1; a2 = 1; #100; a1 = 1; a2 = 0; #100; a1 = 0; a2 = 1; #100; a1 = 0; a2 = 0; end endmodule
[디지털 시냅스의 설계]
디지털 시냅스의 설계를 위한 주요 사항
1. 신호 전달 방향
디지털 시냅스는 입력과 출력을 가지며, 신호의 전달 방향을 결정해야 한다.
양방향으로 신호를 전달하는 것도 가능하지만, 대부분의 경우 입력과 출력을 명확히 구분하여 설계한다.
2. 디지털 논리
디지털 시냅스는 디지털 논리 게이트로 구성된다.
AND, OR, NOT 등의 게이트를 조합하여 원하는 논리 기능을 수행하는 디지털 논리 회로를 설계해야 한다.
3. 시냅스 강도 조절
시냅스의 강도를 조절하는 매커니즘을 포함해야 한다.
이는 입력 신호에 대한 출력의 영향력을 결정하는데 중요한 역할을 한다.
4. 시냅스의 상태
디지털 시냅스는 상태를 가질 수 있으며, 이는 학습 및 기억에 사용된다.
시냅스의 상태를 적절히 관리하여 원하는 동작을 구현해야 한다.
5. 시냅스의 타이밍
디지털 시냅스는 clock 신호를 기반으로 동작하므로 시냅스의 타이밍을 잘 조절해야 한다.
이는 입력과 출력의 변화가 올바른 시점에서 발생하도록 보장하는데 중요하다.
6. 에너지 효율성
디지털 시냅스는 에너지 효율성을 고려하여 설계해야 한다.
효율적인 에너지 사용은 대규모 네트워크나 인공지능 시스템에서 중요한 고려사항 중 하나이다.
7. 노이즈 및 오류 처리
디지털 시스템은 외부 노이즈나 오류에 민감할 수 있으므로 이를 처리하는 방법을 고려해야 한다.
에러 보정 매커니즘 등을 적용하여 신뢰성을 향상시킬 수 있다.
메모리 기반의 Weights 저장
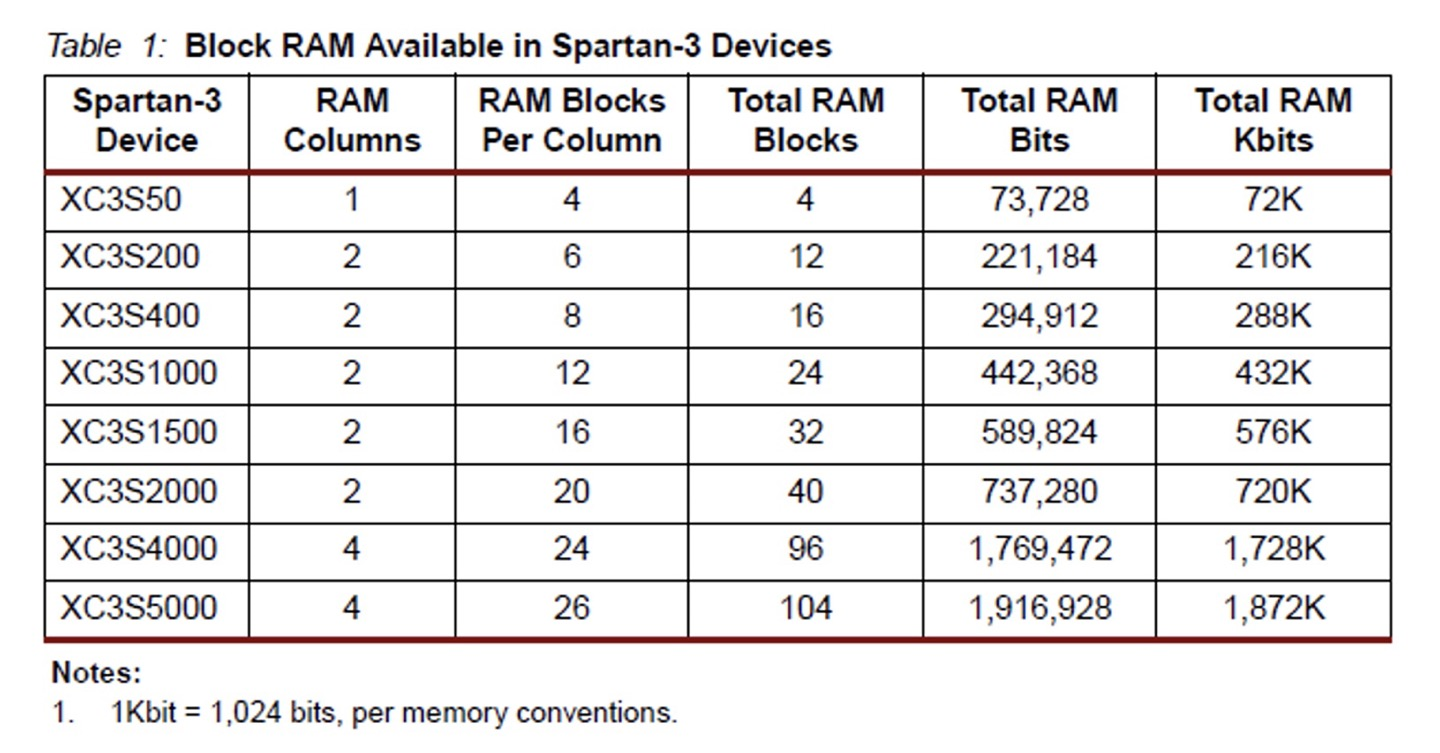
대부분의 디지털 시냅스에서는 가중치를 저장하기 위해 메모리를 사용하며,
Xilinx와 같은 기업은 다양한 메모리 블록을 제공하여 이를 구현할 수 있도록 지원한다.
대표적인 예시로 RAMB16BWER(18 Kb)과 RAMB8BWER(9Kb) 같은
메모리 기본 요소(Primitive cell)이 제공되며, 가중치를 저장하는데 사용된다.
이런한 메모리 기반 가중치 저장 방식은 뉴런의 수가 적을 때는 적은 영역을 차지하지만,
뉴런의 수가 많아질수록 필요한 메모리 공간이 급격히 증가하게 된다.
위와 같은 저장방식은 Register처럼 사용하면 된다.
ex)
reg [39:0] mem1 [0:255]; // 256 40-bit register
initial $readmemb("file1", mem1);
- 종류
$readmemb(2진수 포맷), $readmemh(16진수 포맷)
- 사용법
$readmemb("파일명", 메모리명, 시작 주소, 마지막 주소)
시그모이드 함수
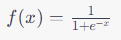
시그모이드 함수란?
주로 인공지능과 머신러닝에서 사용되는 비선형 활성화 함수 중 하나이다.
이 함수는 입력값을 0과 1사이의 값으로 변환해주는 S모양의 곡선을 가지고 있으며,
주로 뉴런의 출력을 제한하는데 사용된다.
시그모이드 함수의 특징
1. 출력 범위
입력값 x가 어떤 실수라도, 시그모이드 함수의 출력은 항상 0과 1사이의 값으로 제한된다.
이는 뉴런의 활성화를 제한하여 출력이 2진 분류 또는 확률값으로 사용될 수 있게 한다.
2. 비선형성
시그모이드 함수는 비선형 활성화 함수로, 입력값에 대한 비선형적인 변화를 제공한다.
이는 다측 퍼셉트론과 같이 비선형 문제를 해결하는데 중요한 역할을 한다.
3. 경사 소실 문제
큰 입력값에 대해 시그모이드 함수의 미분값은 매우 작아질 수 있다.
이로 인해 역전파(Back propagation) 알고리즘을 사용하는 딥러닝 모델에서
기울기 소실(Gradient Vanishing) 문제가 발생할 수 있다.
최근에는 ReLU(Rectified Linear Unit)와 같은 다른 활성화 함수들이 널리 사용되고 있으며,
시그모이드 함수는 특히 출력층에서 2진 분류 문제나 특정 범위로 제한된 출력이 필요한 경우에 사용된다.
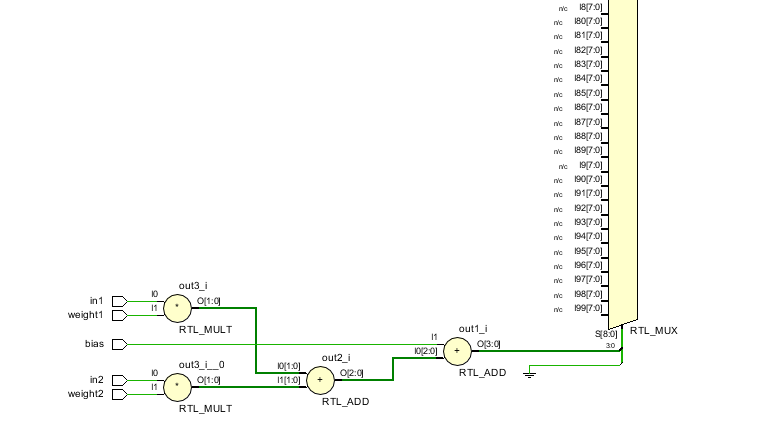
시그모이드 함수를 활용한 뉴런 설계
뉴런은 입력에 가중치를 곱한 값을 모두 더하고,
그 결과에 bias를 더한 값을 시그모이드 함수의 근사값으로 출력한다.
이렇게 구현된 뉴런은 입력과 가중치를 조합하여 출력값을 생성하며,
이를 통해 인공 신경망이나 다른 디지털 신호처리 애플리케이션에서 사용될 수 있다.
module Neuron_sigmoid( input clk, in1, in2, weight1, weight2, bias, output reg out ); reg weighted_sum; always @(*) begin // 입력과 가중치를 곱하여 가중합 계산 weighted_sum = in1 * weight1 + in2 * weight2; end always @ (posedge clk) begin // 시그모이드 함수를 사용하여 출력 계산 out <= 1 / (1+ exp(-weighted_sum - bias)); end endmodule
위와 같이 exp 함수를 쓰면 편하겠지만,
시그모이드 함수는 지수 함수 eⁿ 을 포함하므로, Verilog에서는 내장된 exp함수를 사용할 수 없다.
대신, 시그모이드 함수를 근사화(Approximation)하는 방법을 사용해야 한다.
일반적으로 하드웨어에서 시그모이드 함수를 근사화하기 위해
Look-up Table(LUT)이나 다른 근사화 기법을 사용한다.
module Neuron_sigmoid_piece_app( input clk, in1, in2, weight1, weight2, bias, output reg out ); reg signed [7:0] weighted_sum; reg [7:0] approx_values [256:0]; // 8bit 입력에 대한 근사값 reg [7:0] i; // 변수 i를 reg로 선언 // Piecewise Linear Approximation을 위한 기울기와 y-절편 계산 localparam [7:0] m = 64; // 기울기 localparam [7:0] b = 32; // y-절편 // 근사값 계산 initial begin for (i = 0; i <= 256; i = i + 1) begin // 변수 i 사용 approx_values[i] = (i * m) + b - bias; end end always @ (*) begin weighted_sum = in1 * weight1 + in2 * weight2 + bias; // bias 연결 end always @ (posedge clk) begin if(weighted_sum >= 0) out <= approx_values[weighted_sum[7:0]]; // 근사값 출력 else out <= approx_values[-weighted_sum[7:0]]; // 1에서 해당 값 뺴기 end endmodule
[Learning Algorithm]
Back Propagation
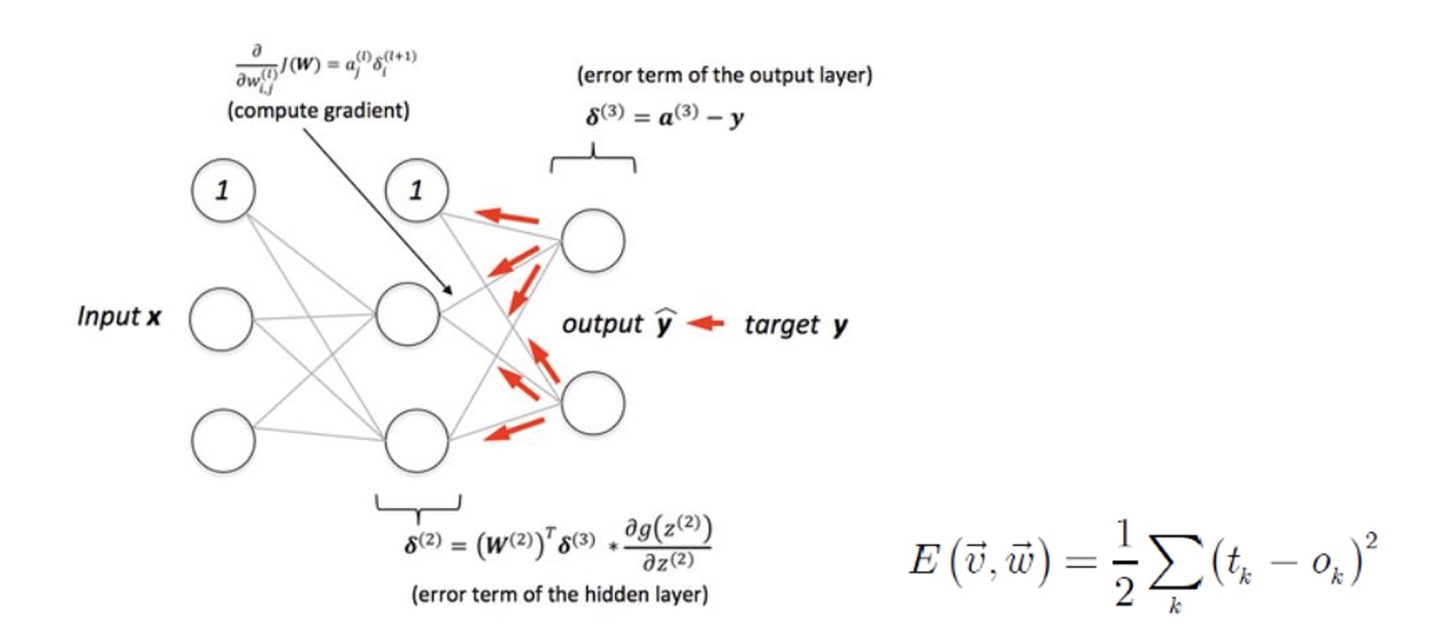
Back propagation(역전파)은 인공신경망에서 학습 알고리즘 중 가장 많이 사용되는 방식 중 하나로,
인공신경망의 가중치(Weight)와 편향(Bias)을 조정하여 원하는 출력에 가깝에 만드는 과정을 말한다.
이 과정은 손실함수(Loss Function)를 최소화하는 방향으로 가중치와 편향을 업데이트한다.
뉴로모픽 시스템의 경우, 학습이 중요하지만 계산량이 많아 대부분 외부에서 수행하는 경우가 많다.
(FPGA에서는 Interface만 수행)
Back propagation은 지도학습(Supervised Learning)에서 사용되며,
다음과 같은 단계로 진행된다.
1) 순전파(Forward Propagation)
: 먼저 입력 데이터를 네트워크에 주입하여 출력을 계산하는 순전파 과정을 거친다.
각 뉴런의 입력과 출력 값을 계산하며, 활성화 함수를 통과한 값을 계산한다.
2) 손실 함수 계산
: 순전파를 통해 얻은 출력값과 실제 정답과의 차이를 계싼하는 손실 함수를 정의한다.
이 손실 함수는 인공신경망이 얼마나 잘 작동하는지 측정하는 척도이다.
3) 역전파(Back Propagation)
: 손실 함수를 최소화하기 위해 가중치와 편향을 업데이트한다.
역전파는 오류를 역방향으로 전파하면서 각 뉴런이 손실 함수에 얼마나 기여하는지 계산한다.
이를 통해 가중치와 편향을 조정하여 손실 함수를 최소화하는 방향으로 이동한다.
4) 경사하강법(Gradient Descent)
: 역전파를 통해 얻은 각 가중치와 편향에 기울기(Gradient)를 사용하여 경사하강법을 수행한다.
경사하강법은 손실 함수가 최소화되는 지점을 찾기 위해
가중치와 편향을 조금씩 조정하는 최적화 알고리즘이다.
5) 가중치와 편향 업데이트
: 경사하강법을 통해 얻은 가중치와 편향을 기울기를 활용하여 실제로 가중치와 편향을 업데이트한다.
학습률(Learning rate)이라는 하이퍼파라미터를 사용하여
얼마나 크게 가중치와 편향을 조절할지를 결정한다.
6) 반복
: 위 과정을 여러 번 반복하여 인공신경망이 최적의 가중치와 편향을 학습하도록 하며,
이를 에포크(Epoch)로 나누어 학습을 수행하게 된다.
특징으로는 뉴로모픽 시스템에 학습을 구현하기 위해 간단한 형태로 구현하며, OR gate를 구현하는 것이 목표이다.
학습 알고리즘을 위해 실수를 사용하며,(1bit - sign, 15bit - 정수, 16bit - 실수)
Adder, Multiplier, Sigmoid 함수를 사용하고 Error는 RMS로 정의한다.
STDP

STDP(Short-Term Plasticity, 단기 가소성)는
시냅스의 가소성(Plasticity) 중 하나로써, 시냅스가 얼마나 오래 유지되는지를 조절하는 학습 규칙이다.
Unsupervised learning의 대표적인 방식이며, 패턴 인식 등에 효과적이다.
STDP는 뉴런 간의 활동에 따라 시냅스의 강도를 조절하며,
두 가지 핵심적인 시간 규칙을 가지고 있다.
1) 시간차에 따른 강화(Long-Term Potentiation, LTP)
: 뉴런 A가 뉴런 B를 먼저 활성화시키고, 그 후에 뉴런B가 뉴런A를 활성화시키면 이때 뉴런 A에서
뉴런 B로의 시냅스의 효율이 증가되며 이러한 상태를 LTP라고 한다.
LTP는 뉴런 간의 연결을 강화시키고, 학습한 정보를 오래 기억하는데 도움을 준다.
2) 시간차에 따른 약화(Long-Term Depressoin, LTD)
: 뉴런 A가 뉴런 B를 먼저 활성화시키고 그 후에 뉴런 B가 뉴런 A를 활성화시키면,
이때 뉴런 A에서 뉴런 B로의 시냅스 효율이 감소한다.
이러한 상태를 LTD라고 하며, LTD는 뉴런 간의 연결을 약화시키고, 불필요한 정보를
삭제하는 데 도움을 준다.
즉, STDP 알고리즘은 spike의 생성에 입력이 기인한 경우에는 연결을 강화하고
그렇지 않은 경우에는 연결을 약화시키는 방법이다.
STDP는 뉴런 간의 활동에 따라 시냅스의 강도를 동적으로 조절함으로써,
학습과 기억에 중요한 역할을 한다.
뇌의 신경회로망에서도 STDP가 발견되어, 학습과 기억의 기본 원리로 간주되고 있고,
딥러닝 모델과 인공신경망에서도 STDP와 유사한 학습 규칙을 활용하여 학습을 시키기 위한
연구가 활발히 진행 중이다.
- Fin -
'# Ai > - Neuromorphic' 카테고리의 다른 글
| <뉴로모픽 시스템에 대하여> Part.2(뉴런 모델, 시냅스 모델, 뉴로모픽 구조) (0) | 2023.07.27 |
|---|---|
| <뉴로모픽 시스템에 대하여> Part.1 (뉴로모픽 컴퓨팅, Neural Network, SNN, 뉴로모픽 칩 등) (0) | 2023.07.26 |

